What is longitudinal data, and why do we need it?

In recent years, the child welfare community has focused attention on the role of longitudinal data analysis. But what are longitudinal data, exactly? Why is the FCDA built on a longitudinal model? And why is longitudinal data analysis the most accurate way to evaluate the experience of children moving through foster care?

At its core, the driving concept behind longitudinal analysis is a simple one: Longitudinal analysis examines change in particular individuals or entities over time. In a child welfare context, this means tracking the experiences of children as they move through the foster care system and interpreting the patterns that are found. Longitudinal analysis provides a way to talk about what happens to children in foster care (e.g., How long do children stay in care? How likely is it that they will re-enter after they exit?) and a way to talk about the extent to which foster care systems on the whole are improving over time (e.g., Is length of stay decreasing? Are rates of re-entry decreasing?).

The best way to highlight why longitudinal analyses provide the most accurate description of outcomes for children in care is to compare them to other types of analyses that provide a biased view.

There are three main types of analytic questions that get posed in child welfare, and each measures a different group of children:

1. Children in foster care: These are the children who make up the active caseload. Analyses of children in foster care are often referred to as point-in-time, cross-sectional, or census analyses.
2. Children who have exited foster care: These are the children who left foster care during a certain time period (usually in the past year). Analyses of children leaving care are often referred to as exit cohort analyses.
3. Children entering foster care: These are the children who enter placement during a certain time period (usually over the course of one year). Analyses of children entering foster care are often referred to as entry cohort analyses.

By definition, these are three very different samples of children. The example below illustrates consequences of studying each by using them to explore two commonly asked questions: What is the length of stay of children in care? And is length of stay increasing or decreasing?

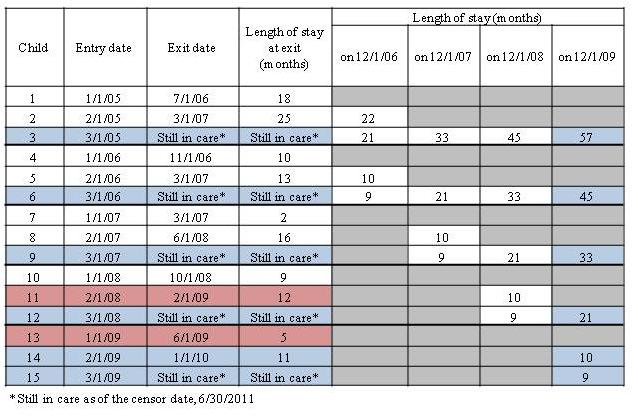
Consider the hypothetical (tiny) foster care system in Figure 1 below. Fifteen children moved through this system between 2005 and 2009; thus, all 15 have an entry date. Some have exited (they have an exit date) and some are still in care as of the censor date, which in this case is 6/30/2011. For all the children who have exited care, their ultimate length of stay is calculable; for those who are still in care, their ultimate length of stay is yet unknown. Additionally, starting in 2006, a census of the in-care population was taken every year on December 1^st and length of stay to date was calculated for all children who were in care on that day.

Figure 1: Length of stay of children in foster care

Let’s say we wanted to examine children’s average length of stay in 2009. An exit cohort analysis would pose the question: Of all the children who exited care in 2009, what was their average length of stay? This analysis would capture the children shaded in red, and their average length of stay would be:

 (12 + 5) ÷ 2 = 8.5 months

In contrast, a point-in-time analysis would pose the following question: Of all children who were in care on 12/1/09, how long had they been in care? This analysis would capture the children shaded in blue, and their average length of stay would be:

 (57 + 45 + 33 + 21 + 10 + 9) ÷ 6 = 29.17 months

And what about length of stay over time? An exit cohort analysis using this group of children would compare the average length of stay of children who exited care in 2009 to the average length of stay of children who exited in 2006, 2007, and 2008. Using the data above, Figure 2 shows that length of stay appears to be decreasing:

 Figure 2: Average length of stay over time—Exit cohort analysis

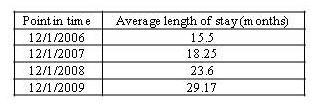
In contrast, a point-in-time analysis would compare the length of stay of children in care on 12/1/2009 to the length of stay of children who were in care on 12/1/2006, 12/1/2007, and 12/1/2008. Taking that perspective, Figure 3 shows that length of stay appears to be increasing:

 Figure 3: Average length of stay over time—Point-in-time analysis

So which is true? Was the average length of stay in 2009 8.5 months or was it 29.17 months? Has length of stay been increasing or decreasing over the years? From these analyses, it’s difficult to say. Exit cohort analyses include only the children who left foster care; therefore, they tend to over-represent the experience of short-stayers, making length of stay seem shorter than it actually is. Point-in-time analyses include only those who remain in foster care; therefore, they tend to over-represent the children who have been in care the longest, making length of stay seem longer than it actually is. The point is: You cannot assess system-wide outcomes if you leave certain children out of your analysis. All children have to be included in a state’s method for monitoring outcomes.

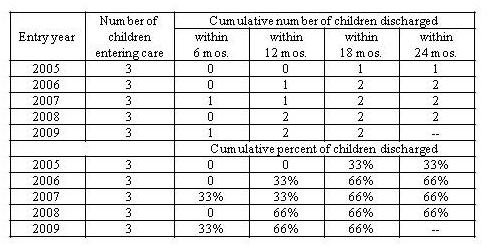
That is why this kind of inquiry calls for an entry cohort analysis—an approach that takes entire cohorts of children entering care and follows all of their members forward as they move through the system (i.e., a longitudinal analysis). Consider the children in our fictitious foster care system above. Regardless of whether they have exited care yet (i.e., as of 6/30/2011), we can fill in the table below based on their length of stay to date. For example, according to Figure 1, three children entered care in 2005—one exited in 18 months, one exited in 25 months, and one is still in care. In other words:

• Zero out of the three 2005 entrants exited within 6 months.    (0 ÷ 3 = 0%)
• Zero out of the three 2005 entrants exited within 12 months.  (0 ÷ 3 = 0%)
• One out of the three 2005 entrants exited within 18 months.   (1 ÷ 3 = 33%)
• One out of the three 2005 entrants exited within 24 months.   (1 ÷ 3 = 33%)

Repeating this process for each entry cohort, we can fill out the table in Figure 4:

 Figure 4: Length of stay—Entry cohort analysis

Of note, this table can’t be filled in completely just yet. As of the censor date, all of the children who entered care in 2009 have not yet had the opportunity to be in care for 24 months; therefore, the proportion of 2009 entrants exiting care within 24 months must be left blank for now.

These percentages would be more varied, of course, if there were more than 3 children in each entry cohort. Figure 5 shows how this table would look in an actual county. The exit time frames are slightly different, but the censor date is still 6/30/2011. Based on these data, what conclusions would you draw about length of stay in this county over the past few years?

 Figure 5: Length of stay—Entry cohort analysis, actual county

Figures 4 and 5 illuminate why an entry cohort analysis is the most comprehensive. We can see that the analysis accounts for all children entering care in each year—in calculating each percentage, the entire entry cohort is always the denominator.

The entry cohort analysis above is just one example of a longitudinal analysis. The Recipes posted in this blog will show you how to perform many others related to permanency outcomes, the effectiveness of interventions, fiscal planning, and the continuous quality improvement process, in general. But what you’ll notice throughout is that all queries involving the measurement of change over time are based on a prospective approach—one that takes a group of children and measures them going forward, rather than one that tries to reconstruct their past.

In the next post, I talk in greater detail about how to frame longitudinal analytic questions. I apply the Data Center’s model to topics other than length of stay, and I discuss how longitudinal analyses fit into the cycle of continuous quality improvement.